Whether you’re trying to secure a loan or calculating the returns of an investment, understanding how the rates are calculated is crucial. The calculation can simply be based on the loan’s principal amount, or it could have a more complex interest-on-interests calculation method.
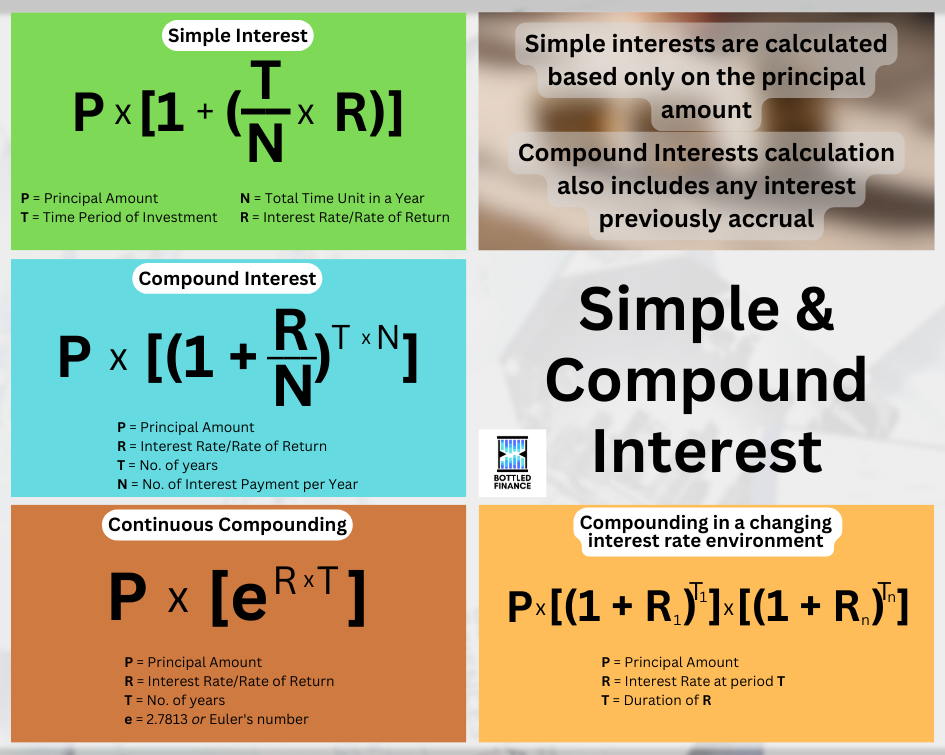
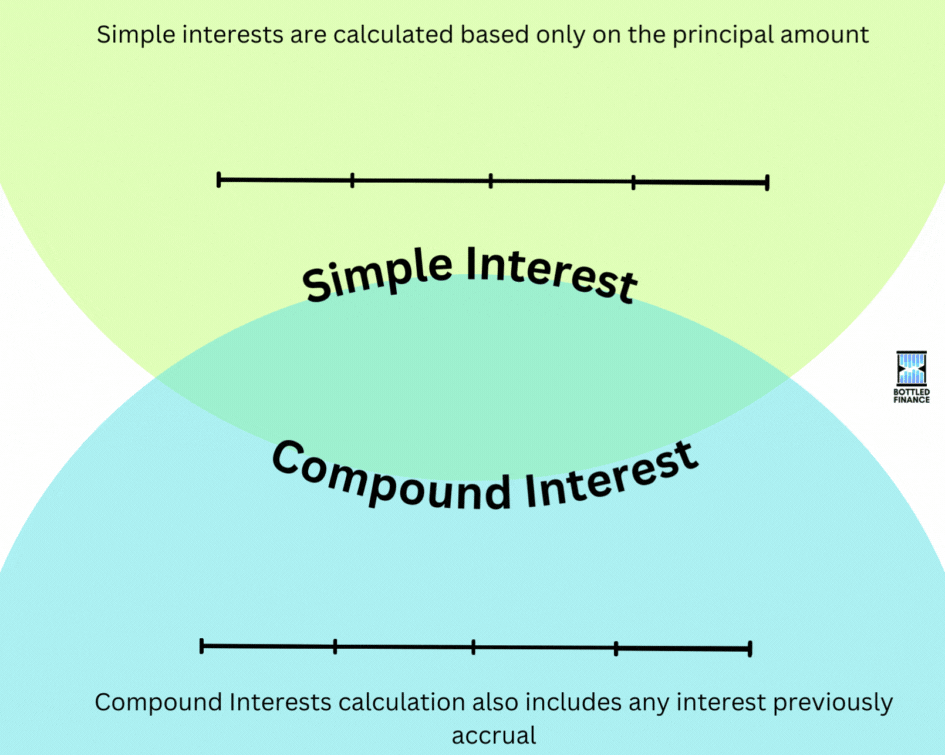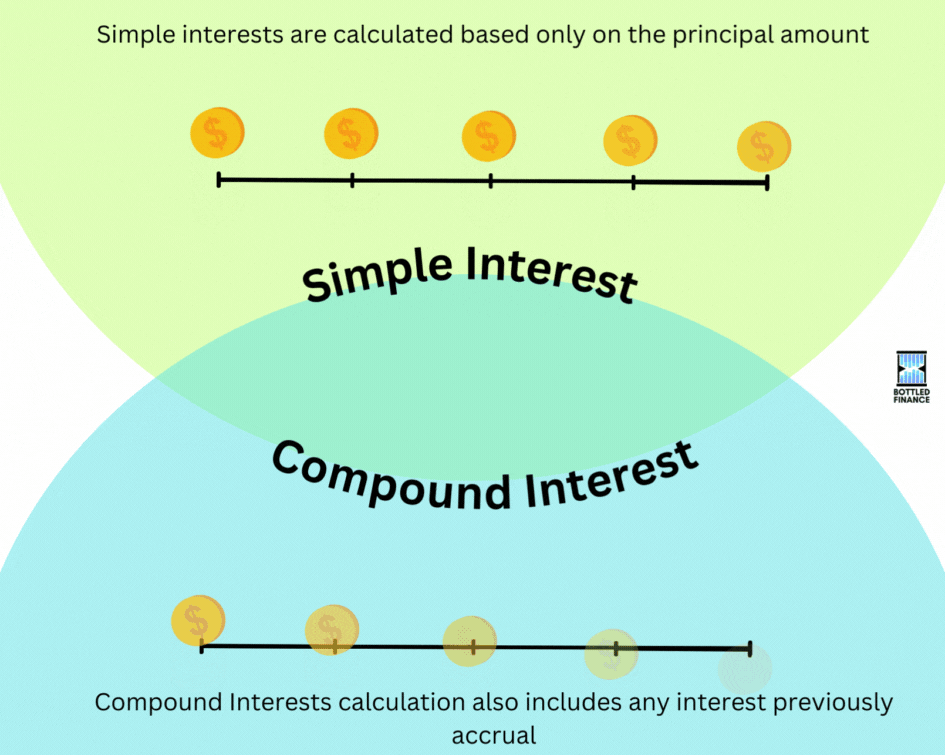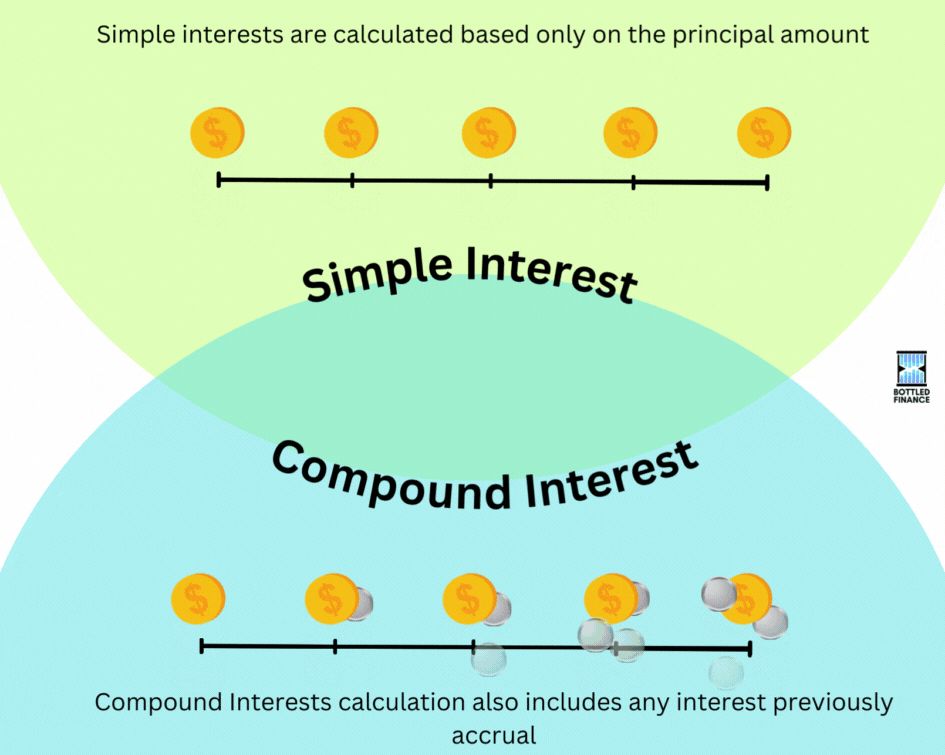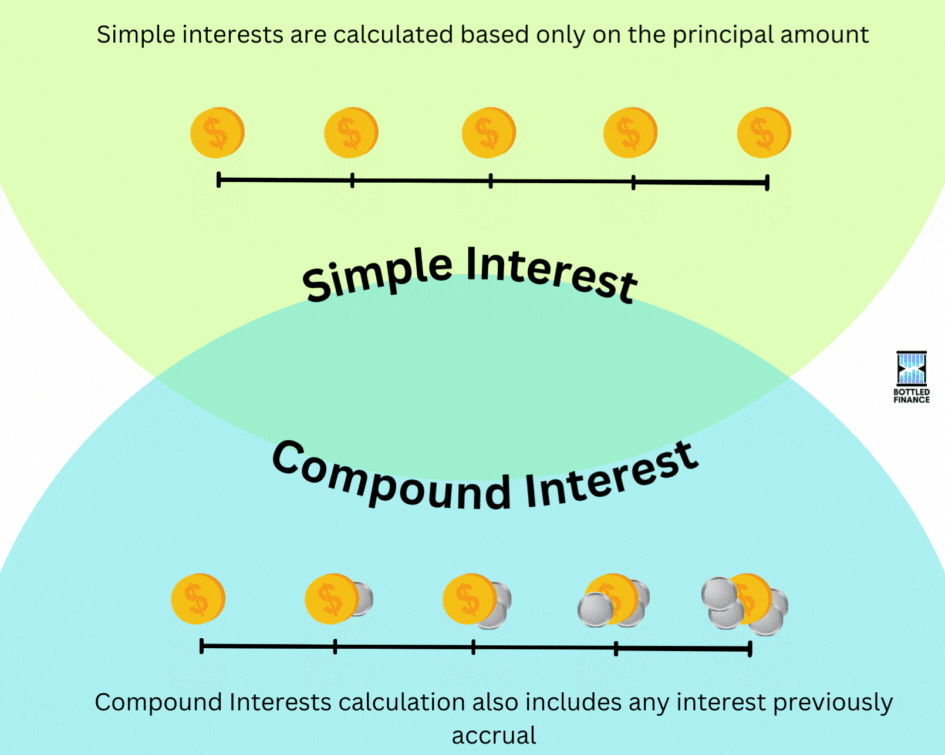
To start, the calculation for Simple interests is based only on the principal amount whereas Compound Interests calculation also includes any interest previously received, interest-on-interest.
Simple Interest

Calculating for simple interest is relatively straightforward: the interest is solely determined by the principal amount.
Calculating the accumulated amount for simple interest requires only three components: the principal amount (P), the number of interest payments (T), and the interest rate (R).

Simple Interest Payment Period (> 1 Year)
The previous example demonstrates a scenario where there is only one coupon payment, and the bond matures in one year, what happens if it was a longer-term bond with more than one coupon payment?
In that case, the frequency of interest payment increases, using the same formula previously presented we can calculate the accumulated amount for a $1,000 loan at a rate of seven percent (7%) that is due in 10 years:

Simple Interest Payment Period (< 1 Year)
What about short-term loans that have a time-to-maturity that is less than a year? Calculating simple interest payments for a duration that is less than a year requires converting and expressing the ‘time’ in relation to years.

The simple interest of a 6-month loan would be expressed as 0.5 years or ½ years (6 months divided by 12 months); for a period of 4 weeks, it would be expressed as 4/52 years (4 weeks divided by 52 weeks); similarly, for an extremely short-term one-day loan, it would be expressed as 1/365 years (1 day divided by 365 days)

Compound Interest
Compound interest is powerful, it could help grow one’s wealth exponentially or it could drastically inflate one’s debt.
Compound interest operates on the principle of interest on interests, previous interests earned are included in the next compounding period; the more times it’s compounded, the more drastic the results would be.
Compounding Period (Once a year)

Similar to simple interest, the formula for compound interest uses the same three components: The principal amount (P), the number of interest payments (T), and the interest rate (R). However, the calculation for compound interest is a little more complex; when calculating compound interest, the number of interest payments (T) is an exponent of the interest rate (R).

Here, we can see the difference between using simple and compound interest calculations. When calculated using the simple interest formula, the Accumulated Amount was calculated to be $1,700, whereas when compounding interest-on-interests, the outcome was an Accumulated Amount of $1,967.15; $267.15 higher.
Compound Interest (More than once per year)
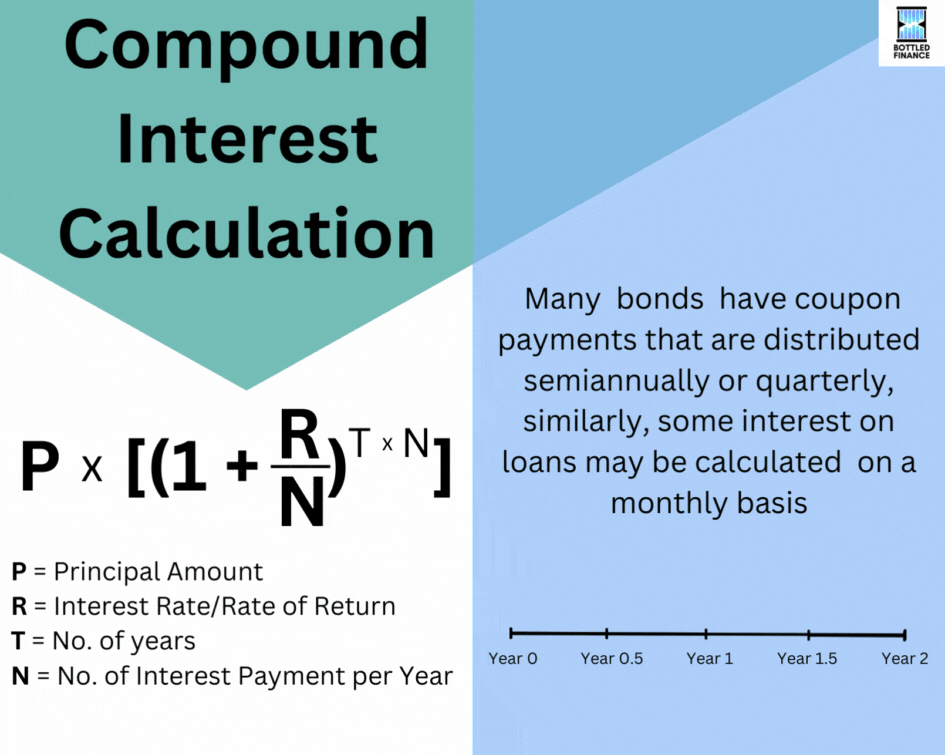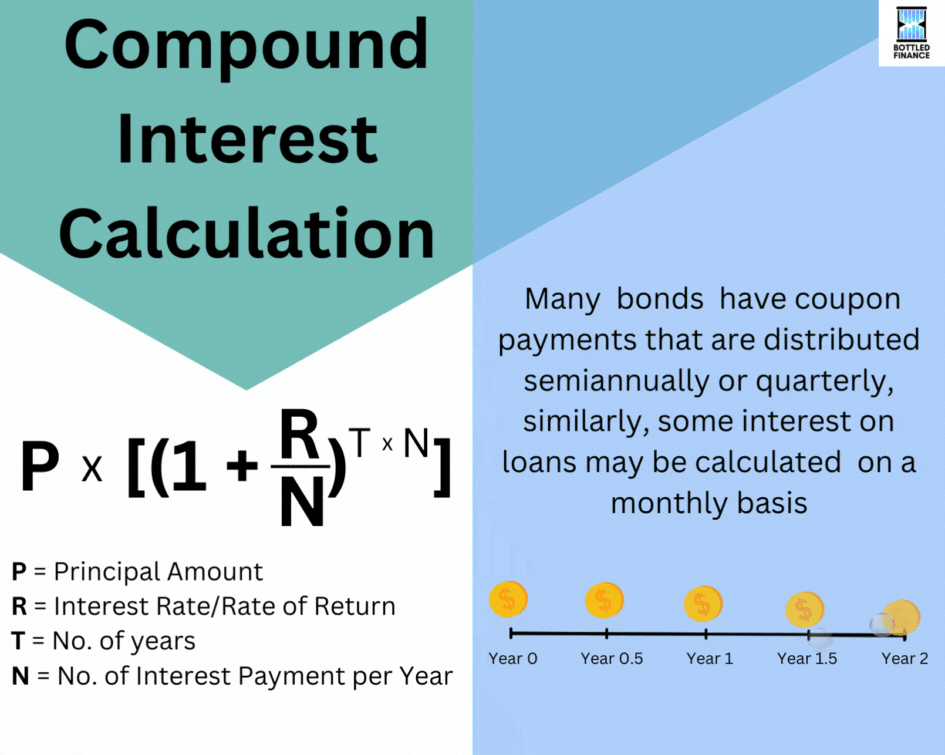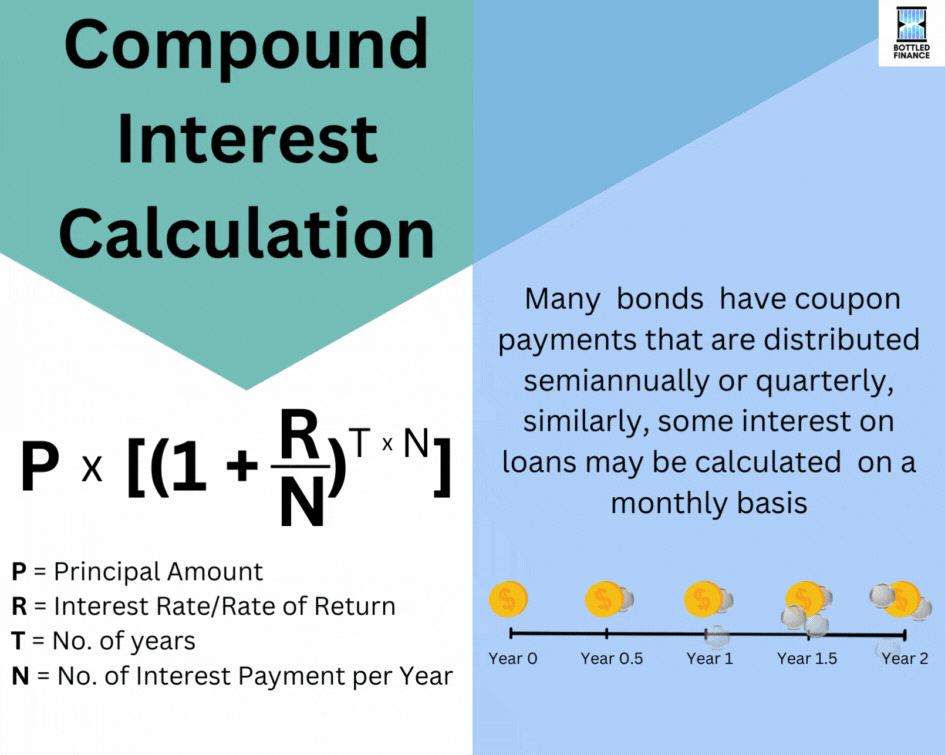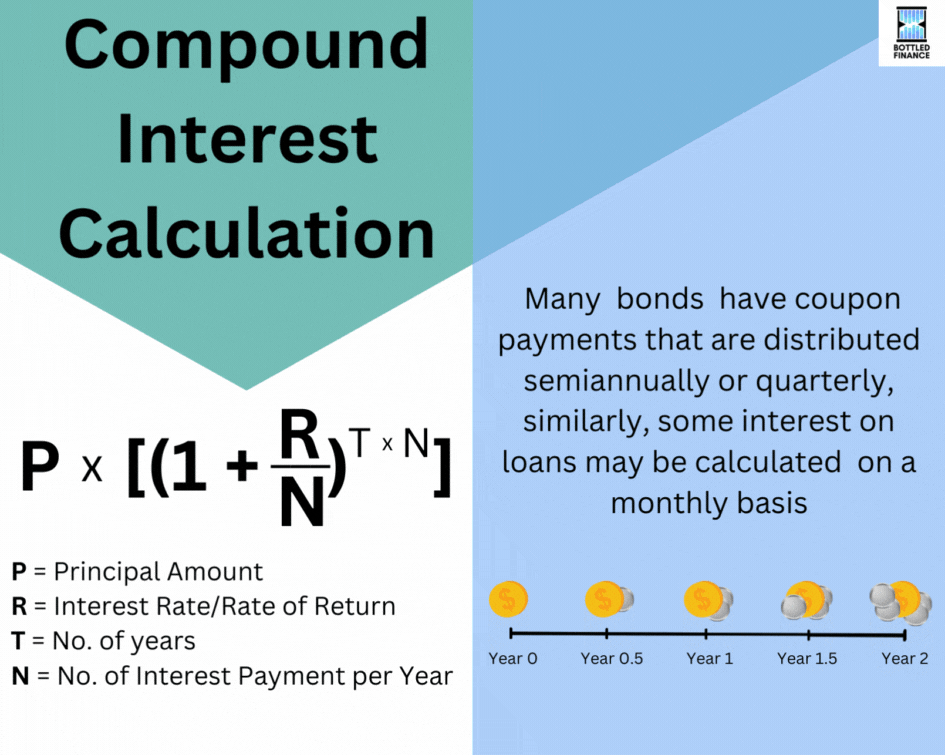
Many bonds have coupon payments that are distributed semiannually or quarterly, similarly, some interest on loans may be calculated on a monthly basis; in those cases, there would be more compounding periods in total.
The formula to calculate compound interest with a compounding period of more than once a year is similar, just slightly expanded; the interest rate (R) now takes into account the number of compounding periods per year and the number of interest payments (T) increases.

From the example, we can observe that by increasing the compounding period, the effective interest rate (EAR) would be greater (7.1225%) than the nominal rate (7%) because the interest-on-interest effect happens earlier and more frequently.
Continuous Compounding
For the sake of simplicity, if the compounding period is so frequent that it can be considered infinite, the formula to calculate the accumulated amount would be:

As an example, if a bank is issuing a loan of $1,000 that is due in a year’s time, with an interest rate of five percent (5%) and a compounding period of incalculable times per second, we can assume that this loan has a continuously compounding period and calculate the Accumulated Amount as:

Compounding in a changing interest rate environment

Some loans and coupon bonds have rates that change according to some external factors, those are known as floating rates or variable rates. A bank may charge two percent (2%) on a mortgage loan for a few years and adjust it to three percent (3%) when the interest rates increase.
Calculating the accumulated amount for an instrument with a floating rate requires us to expand the compound interest formula. We’re able to figure out the accumulated amount for a floating rate loan by multiplying the principal amount (P) by the initial interest rate (R1) with an exponent of the duration when the initial interest rate is in effect (T1), multiplied by the next interest rate (R2) with an exponent of the duration of the next interest rate (T2), and so on.

Conclusion
Understanding the differences between simple interest calculation and compound interest calculation is crucial for investors and laypersons alike; it allows borrowers to evaluate the total amount of repayment or helps investors interpret the future value of certain investments.
Compound interest is a powerful tool. For it to work against you, it’s dreadful. However, for it to work for you, it’s impressive.
References
Jothi, A. L. (2009). Financial mathematics. Himalaya Publishing House.
Leibowitz, M. L., Homer, S., & Kogelman, S. (2013). Inside the yield book : The classic that created the science of bond analysis. John Wiley & Sons, Incorporated.
Richelson, H., & Richelson, S. (2011). Bonds : The unbeaten path to secure investment growth. John Wiley & Sons, Incorporated.

