The Rule of 72 is a simple and straightforward way of estimating the duration required for an investment to double, given a known rate of return (Spitzer & Singh, 1999; Cuddington, 2002; Sokunbi, 2020).
Formula and Calculation

To estimate the time (in years) required for an investment to double in value, simply divide 72 by the expected rate of return:
Duration Required = 72 ÷ Rate of Return
(Malkiel & Ellis, 2013; Spitzer & Singh, 1999; Sokunbi, 2020).
Applications of the Rule
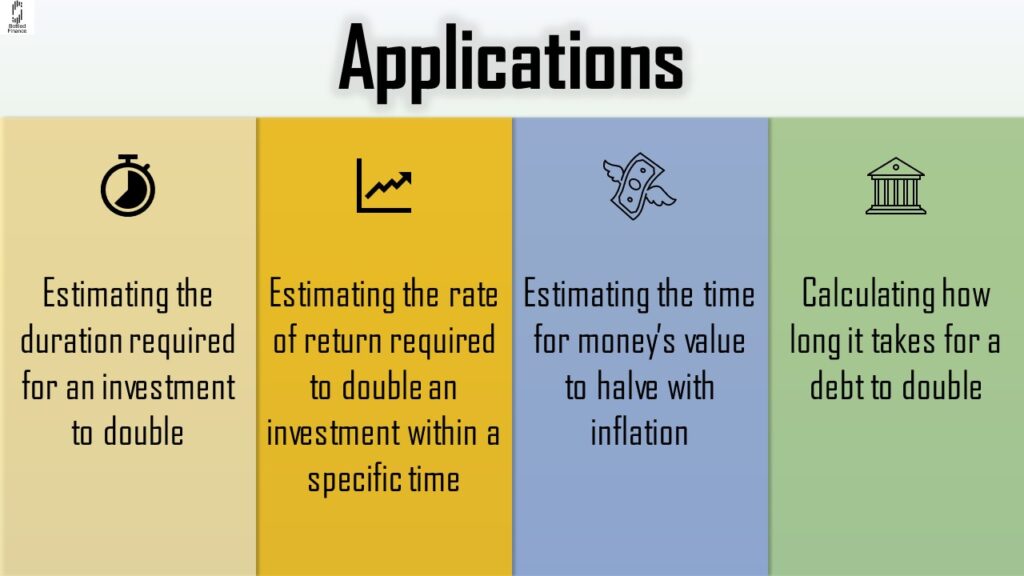
Estimating the duration required for an investment to double
The Rule of 72 offers a convenient way for investors to estimate how long it takes for an investment to double in value based on a given rate of return (Cuddington, 2002).
For example, if the rate of return on an investment is 3.5% (compounding), using the Rule of 72, the estimated duration for the investment to double in value is around 20.6 years (72 ÷ 3.5% = 20.6 years).
Estimating the rate of return required to double an investment within a specific time
It can also be used to estimate the rate of return required for an investment to double, given a desired investment horizon (Cuddington, 2002).
If an investor has a five-year horizon, their investments must generate around 14.4%, compounded annually, to observe a 100% return (72 ÷ 14.4% = 5 years).
Estimating the time for money’s value to halve with inflation
On the other hand, figuring out how long it takes for money to lose half its value only requires the rate of inflation (Sokunbi, 2020).
Assuming a country’s rate of inflation is 2%, the Rule of 72 estimates that its currency would lose half its value roughly every 36 years (72 ÷ 2% = 36 years).
Calculating how long it takes for a debt to double
Given a fixed interest rate, the Rule of 72 can give a rough estimate as to when a loan amount would double (Sokunbi, 2020).
Assuming the interest rate of a credit card loan is 18%, it would only take around four years for the debt to double in value (72 ÷ 18% = 4 years).
Limitations of the Rule
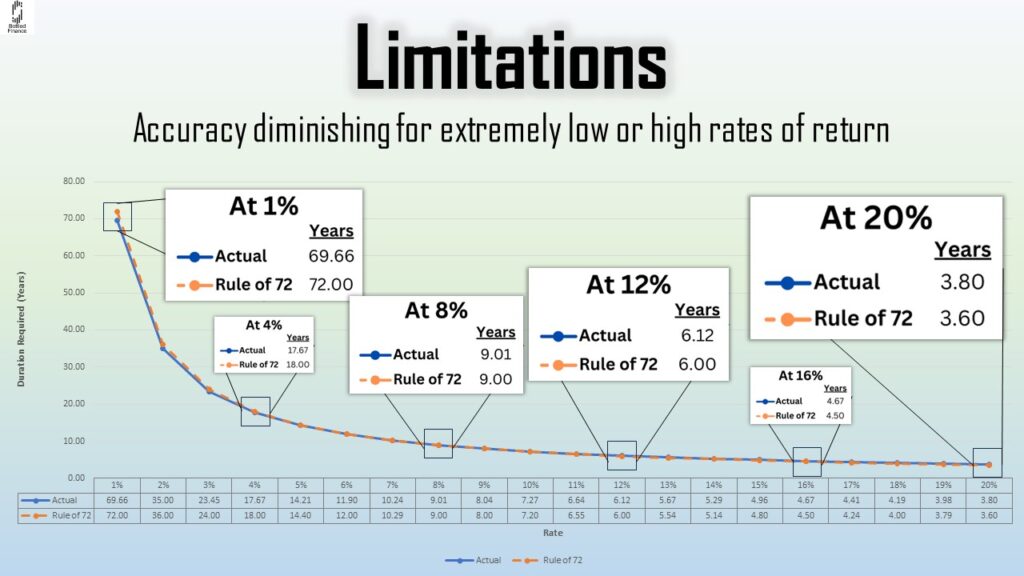
Spitzer and Singh (1999) and Cuddington (2002) suggest that the Rule of 72 is most reliable for interest rates between 6% and 12%, with its accuracy diminishing for extremely low or high rates of return.
Alternatives to the Rule
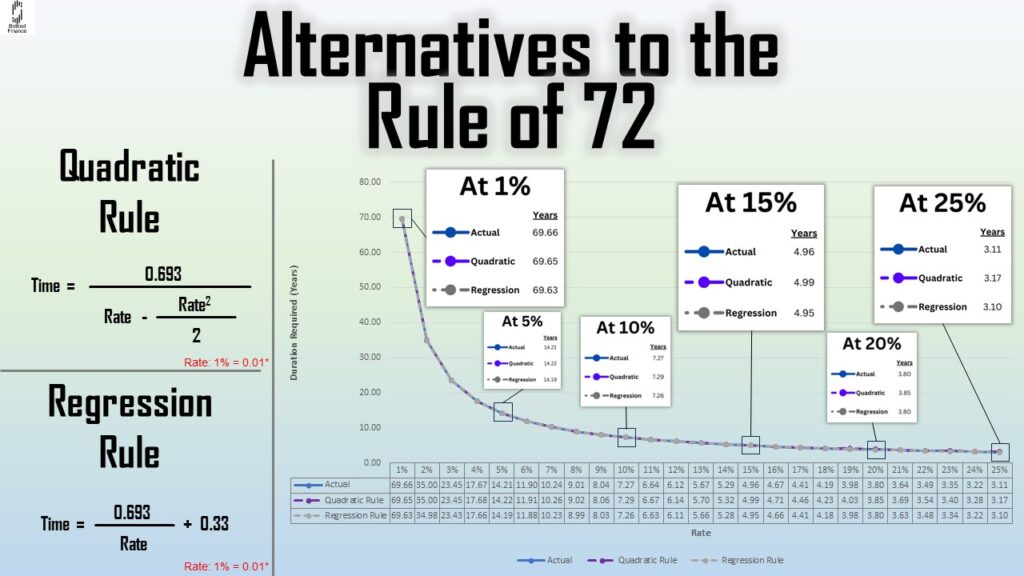
The Quadratic Rule
Spitzer and Singh (1999) proposed using the Quadratic Rule as an alternative to calculate the duration it takes for an investment to double, with the formula being:
Duration required for an investment to double in value = 0.693 ÷ [rate – (rate2 ÷ 2)]
The Regression Rule
The Regression Rule is also a good alternative as it is accurate when measuring rates between 1% – 50% (Spitzer & Singh, 1999).
Using the Regression Rule the time for an investment to double is calculated as follows:
Duration required for an investment to double in value = (0.693 ÷ Rate) + 0.33
(Spitzer & Singh, 1999)
Concluding Remarks
The Rule of 72 and its alternatives are effective approaches to estimating the duration required for an investment or a loan to double in value.
Its simplicity and ease of use allow individuals to evaluate the viability of an investment given a specific rate of return or the weight of an interest rate on its loan.
However, the accuracy of this rule weakens when measuring very high or low rates. Therefore, it has been proposed that employing the quadratic and regression rules would generate more accurate results in such situations.
It is important to note that the rule and its alternatives are measures of estimation that might often deviate from the true value. Thus, it may not be reasonable to base investment decisions solely on the estimations derived from these rules.
References
Cuddington, J. T. (2002). A technical fix for the rule of 72…or is it the rule of 69? Journal of Financial Service Professionals, 56(6), 36.
Malkiel, B. G., & Ellis, C. D. (2013). The elements of investing : easy lessons for every investor (2nd ed.). Wiley.
Sokunbi, B. (2020). Clever Girl Finance. John Wiley & Sons, Incorporated.
Spitzer, J. J., & Singh, S. (1999). The Rule Of 72? Financial Counseling and Planning, 10(1), 1-3.
Other Useful Readings
Ijiri, Y. (1972). Approximations to Interest Formulas. The Journal of Business (Chicago, Ill.), 45(3), 398–402. https://doi.org/10.1086/295468